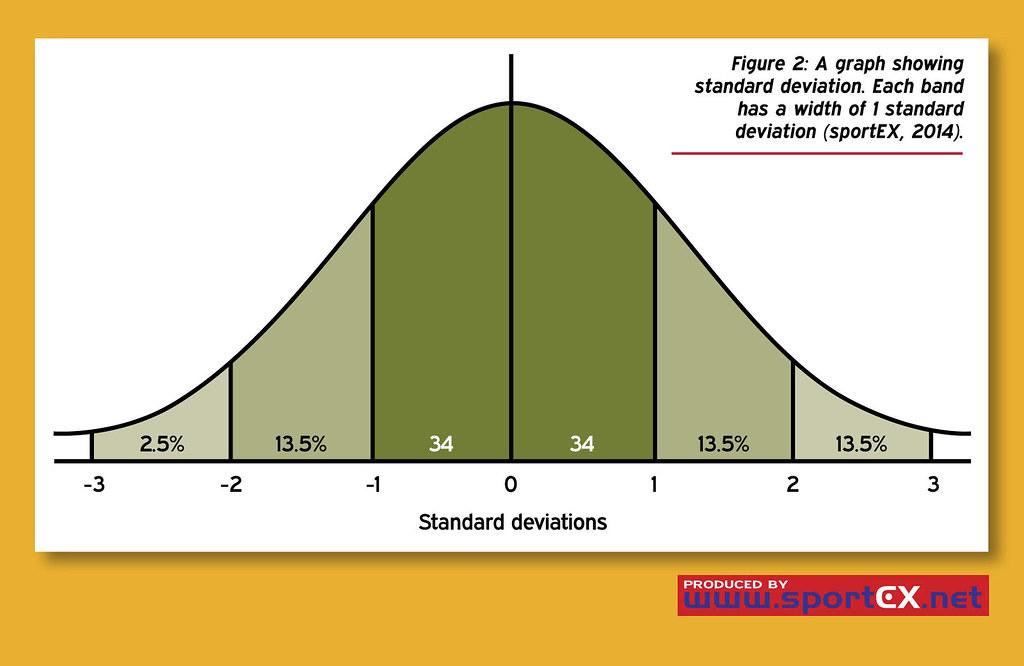
I en verden full av data og statistikk, er standardavvik en nøkkelkomponent for å forstå og tolke informasjon på en meningsfull måte. Enten du er en matematiker, økonom, eller bare en nysgjerrig sjel, er det viktig å ha en god forståelse av hva standardavvik egentlig er. I denne artikkelen skal vi utforske begrepet og utforske hvordan det kan hjelpe oss med å analysere og tolke data på en effektiv måte. Så hva er egentlig standardavvik? La oss finne ut!
Hvordan beregnes standardavvik?
Standardavvik er en statistisk beregning som brukes for å måle spredningen av data i forhold til gjennomsnittet. Det gir oss et mål på hvor mye individuelle verdier i datasettet avviker fra gjennomsnittet. Beregningen av standardavvik er viktig i statistikk for å forstå hvor variabelt dataene er og for å kunne sammenligne ulike datasett.
For å beregne standardavvik, følger vi disse trinnene:
- Finn gjennomsnittet av datasettet.
- Subtraher gjennomsnittet fra hver verdi i datasettet.
- Summer kvadratet av disse differansene for å få summen av kvadrerte avvik.
- Divide summen med antall observasjoner minus 1.
- Til slutt, ta kvadratroten av dette for å få standardavviket.
Fordeler med å bruke standardavvik
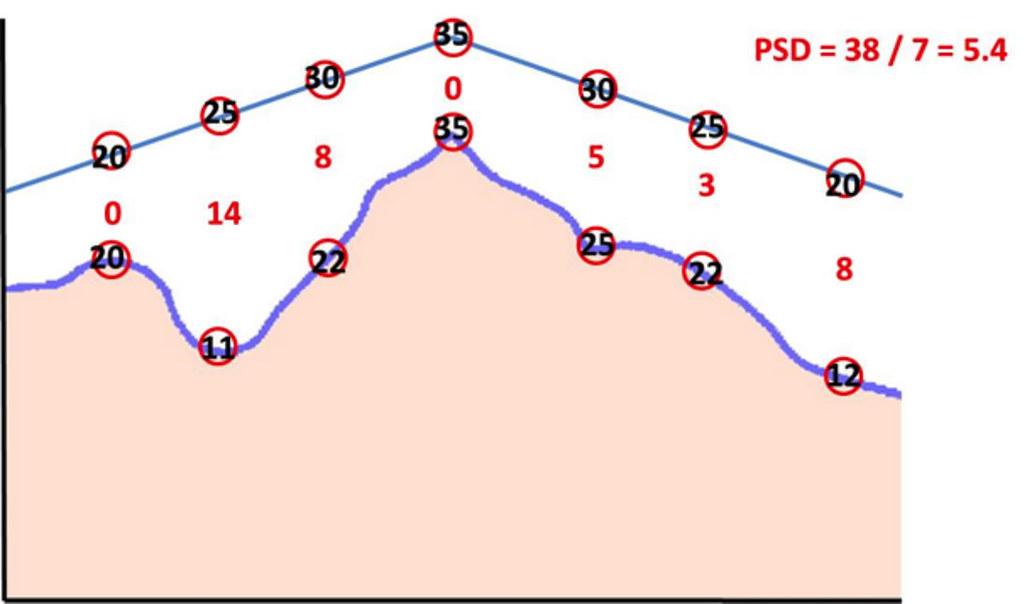
Standardavvik er et begrep som brukes i statistikk for å måle spredningen av dataene i forhold til gjennomsnittet. Ved å bruke standardavvik kan man få en bedre forståelse av hvor mye verdiene i datasettet avviker fra gjennomsnittet. Her er noen :
- Viser variasjon: Standardavviket gir en indikasjon på hvor spredt dataene er rundt gjennomsnittet, noe som er nyttig for å forstå variasjonen i datasettet.
- Sammenlignbarhet: Ved å beregne standardavvik kan man enkelt sammenligne spredningen av ulike datasett, uavhengig av enhetene som brukes.
- Identifiserer outliers: Standardavviket kan hjelpe med å identifisere ekstreme verdier i datasettet som kan påvirke analysen og resultatene.
Anbefalinger for tolkning av standardavvik
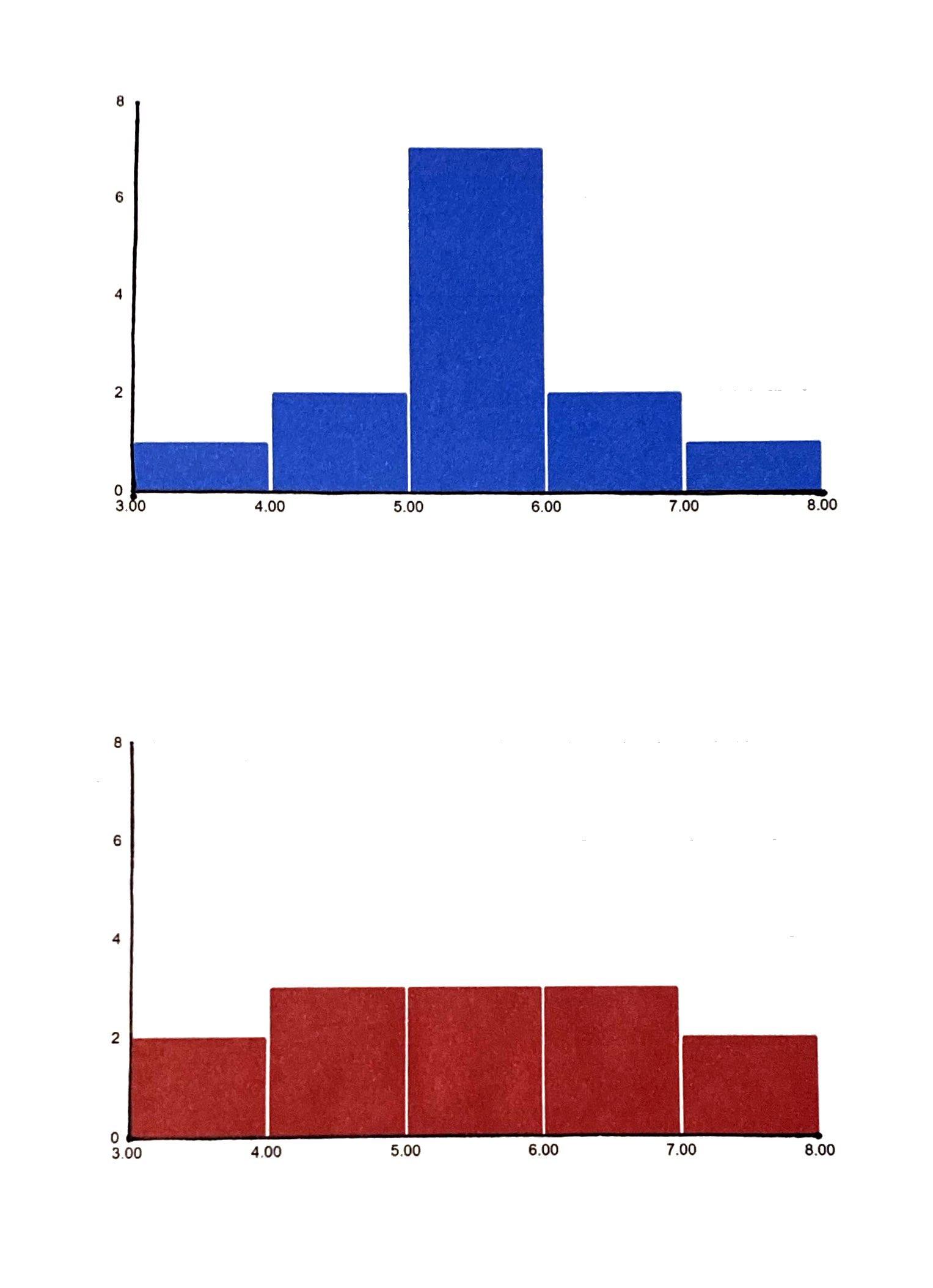
Standardavvik er et mål på spredningen av data i forhold til gjennomsnittet. Det forteller oss hvor mye de individuelle dataene avviker fra gjennomsnittet av datasettet. Her er noen :
- Jo høyere standardavvik, desto større spredning: Et høyt standardavvik indikerer at dataene i datasettet er spredt over et større område.
- Jo lavere standardavvik, desto mindre spredning: Et lavt standardavvik indikerer at dataene ligger tettere rundt gjennomsnittet.
- Sammenligning av standardavvik: Standardavviket kan brukes til å sammenligne spredningen av data mellom ulike datasett eller grupper.
Vi håper denne artikkelen har gitt deg en bedre forståelse av hva standardavvik er og hvorfor det er viktig innen statistikk. Ved å ta hensyn til standardavviket kan du bedre tolke data og fatte informerte beslutninger. Enten du er en erfaren statistiker eller bare nysgjerrig på emnet, er det alltid nyttig å ha kunnskap om standardavvikets rolle i analysen av data. Fortsett å utforske og lære, og la standardavviket veilede deg i dine statistiske eventyr. Tusen takk for at du leste!